Photonic and plasmonic crystals

The broad range of photonic crystal applications is based on their photonic bandgaps, which enable the design of various waveguides, cavities, mirrors, switches, and filters. On the other hand, a tunable dispersion within allowed bands can be useful as well. It can be used for highly dispersive prism, superprism, self-collimation, self-guiding and negative refraction.
While the inherent property of photonic crystals is a periodic arrangement of their unit cells, inhomogeneous and graded photonic crystals consist of unit cells with spatially varying geometrical and/or material properties. Graded photonic crystals with appropriate gradation of the unit cells within the space can be used for light bending and focusing. In this way, graded photonic crystals further expand and enhance the applicability of photonic crystals for light manipulation within allowed bands.
Our research in photonic and plasmonic crystals includes the following fields:

1. engineering of their equifrequency contours in order to achieve negative refraction, self-collimation and guiding of light,
2. graded photonic and plasmonic crystals in order to implement specified gradient refractive index profiles.

 

All-angle left-handed negative refraction in Kagomé and honeycomb lattice photonic crystals

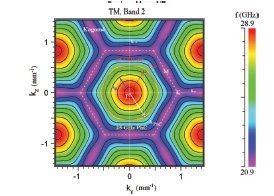
The band structure of a 2D Kagomé GaAs rod photonic crystal for r /a=0.27. The dashed line corresponds to the light line and the gray strip denotes the region with AALNR in the TM2 band.	The equifrequency contours of the TM2 mode for a 2D Kagomé GaAs rod photonic crystal. The red circle denotes the air 25 GHz EFC f ( =0.183), whereas the yellow thick contour is a PhC EFC at the same frequency. EFCs are presented for 22, 23, ..., 28, and 28.7 GHz.	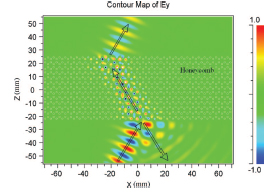The wave pattern of the 25 GHz TM2 EMW propagating through a Kagomé GaAs rod photonic crystal at the 34° incidence across the gammaK interface (FDTD).	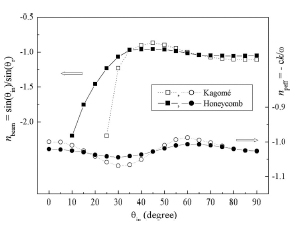The effective indices, nbeam and npef f, of both lattices at 25 GHz(Kagomé) and 26 GHz (honeycomb) as a function of the incident angle.

Possibilities of all-angle left-handed negative refraction in 2D honeycomb and Kagomé lattices made of dielectric rods in air are discussed for the refractive indices 3.1 and 3.6. In contrast to triangular lattice photonic crystals made of rods in air, both the honeycomb and Kagomé lattices show all-angle left-handed negative refraction in the case of the TM2 band for low normalized frequencies. Certain advantages of the honeycomb and Kagomé structures over the triangular lattice are emphasized. This especially concerns the honeycomb lattice with its circlelike equifrequency contours where the effective indices are close to −1 for a wide range of
incident angles and frequencies.Figure 2. Self-collimation waveguide (SCW) designed on the (3.12.12) 2D Archimedean lattice (GaAs cylinders in the air) that gives propagation through the structure without spatial wave dispersion. Results are obtained with the FDTD numerical simulations.

References
Radoš Gajić, Ronald Meisels, Friedemar Kuchar, and Kurt Hingerl “All-angle left-handed negative refraction in Kagomé and honeycomb lattice photonic crystals”, PRB 73, 165310 (2006)

Negative refraction

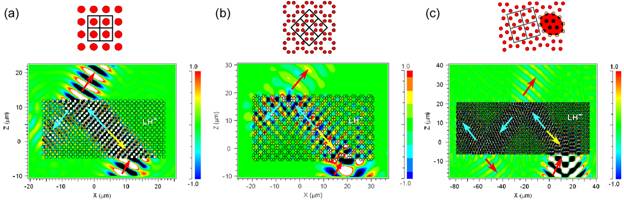
Figure 1. Left handed negative (LH-) refraction in the a) square, b) parquet (4.8.8) and c) ladybug (3.3.4.3.4), 2D Archimedean lattices (GaAs cylinders in the air). For the same excitation wave parameters almost the same optical response (10% deviation for the refracted angle) for all tree structures is obtained. This is the consequence of the similarity in the space symmetry class (square one) of the structures. The red, blue and yellow vectors stand for air, group and phase wave velocity, respectively. Results are obtained with the FDTD numerical simulations.
References
Dj. Jovanović, R. Gajić, K. Hingerl, "Refraction and band isotropy in 2D square-like Archimedean photonic crystal lattices", Opt. Express 16, 4048 (2008).

R. Gajić, Dj. Jovanović, K. Hingerl, R. Meisels and, F. Kuchar “2D photonic crystals on the Archimedean lattices (tribute to Johannes Kepler (1571-1630))”, Opt. Mater. 30, 1065 (2008).  

Dj. Jovanović, R. Gajić, "Optical properties of the (3.4.6.4) hexagonal Archimedean photonic crystal", J.  Nanophotonics 5, 051820 (2011).

Graded photonic crystals
Engineering of a refractive index profile is a powerful method for controlling electromagnetic fields. In order to fabricate broadband and low-loss gradient refractive index media (GRIN) media at optical frequencies, dielectric media should be used. We investigate possible realization of isotropic gradient refractive index media using two-dimensional graded photonic crystals. They consist of dielectric rods with spatially varying radii or air holes with spatially varying radii in homogeneous dielectric background. The graded photonic crystals can be homogenized in broad frequency range within the lowest band. Here they operate in metamaterial regime, that is, the graded photonic crystals are described with spatially varying effective refractive index so they can be regarded as low-loss and broadband graded dielectric metamaterials.

 

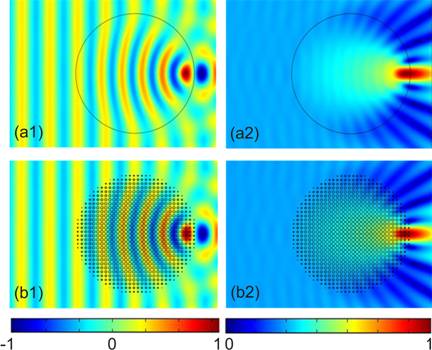
Figure 3. Finite element method simulation results of TE mode (electric field is normal to rods) for (a) the Luneburg lens and (b) the graded photonic crystal based Luneburg lens. On the left side, (x1), the z-component of magnetic field is shown and on the right side, (x2), the magnetic field intensity

References

B. Vasić, G. Isić, R. Gajić, K. Hingerl, "Controlling electromagnetic fields with graded photonic crystals in metamaterial regime", Opt. Express 18, 20321 (2010).

B. Vasić, R. Gajić, "Self-focusing media using graded photonic crystals: Focusing, Fourier transforming and imaging, directive emission, and directional cloaking", J. Appl. Phys. 110, 053103 (2011).

 

Tunable graded plasmonic crystals

In order to implement tunable gradient refractive index devices, we investigate two-dimensional graded plasmonic crystals with semiconductor rods which operate at terahertz frequencies. Radii of rods are spatially dependent and in the effective medium approximation, the graded plasmonic crystals can be considered as effective media with a graded effective dielectric permittivity. The semiconductor rods have the Drude-type dispersion. By varying free charge carrier concentration in the rods, it is possible to tune their permittivity. In accordance to effective medium theory, the effective permittivity of the whole graded plasmonic crystals is changed at the same time. In particular, these graded plasmonic crystals can be made invisible to the incoming radiation by equaling the real part of the rods permittivity to the permittivity of air background.

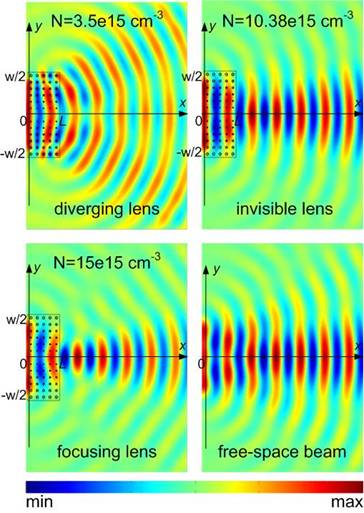
Figure 4. Simulation results for the z component of electric field at 2 THz. By increasing charge carrier concentration N in InSb rods, it is possible to achieve diverging lens, invisible and focusing lens.

References

B. Vasić, R. Gajić, "Tunable gradient refractive index optics using graded plasmonic crystals with semiconductor rods", J. Opt. Soc. Am. B 29, 79 (2012)